En la última parte del curso vamos a estudiar unos conceptos sencillos de estadística y probabilidad.
Primero el mapa conceptual de la unidad:
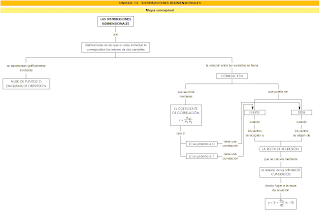
Unos enlaces para repasar la estadística:
Introducción a la estadística - Monografias.com
Elementos de probabilidad y estadística
Estadística 2º de Bachillerato - WikiDdS
Para consultar ejercicios sobre estadística, podéis revisar:
¤ Tema 13 Distribuciones bidimensionales
¤ Estadística
¤ Estadística (II)
¤ Estadística (III)
¤ Estadística (IV)
¤ Tema 13 Soluciones
Todas las soluciones de los ejercicios (del libro del año pasado) y las del libro de este año.
jb
