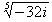Ejercicios tema 8 (II)

Veamos ahora algun ejercicio sobre ecuaciones de la recta

Examen recuperación vectores

1) Observa el rombo de la figura

y calcula:
a) AB + BC
b) OA + OD
c) AD – AB
d) Expresa OC como combinación lineal de BA y BC
Expresa los resultados utilizando los vértices del rombo.
Solución

2) Dados los vectores a(–1, 3), b(7, –2):
a) Calcula un vector c tal que b = 3a – 1/2·c
b) Expresa el vector u(5, 4) como combinación lineal de a y b.
Solución

3) Dados los vectores a = 2u – v y b = u + kv, siendo u(3, 2) y
v(–1, 3), hallar k de modo que (a + b) sea ortogonal a (a – b).
Solución

4) Dado el vector u(5, 12) halla:
a) los vectores perpendiculares a u y de su mismo módulo.
b) el valor de a sabiendo que v(a, 4) forma un ángulo de 45º con u.

5) Si |u| = 6, |v| = 4 y |u + v| = 8, ¿qué ángulo forman u y v? ¿Cuánto vale |u – v|?
Solución

Ejercicios Tema 8 (I)

Este tema es muy amplio en aplicaciones prácticas y problemas (en el libro hay 108 ejercicios), pero en contenidos es mucho más restringido.

Es importante conocer los puntos básicos del tema:

1) Analizar qué relaciones existen entre puntos, rectas y vectores
2) Calcular distancias y ángulos, interpretándolos correctamente.

Si conocemos bien estos puntos podemos resolver cualquier problema geométrico, incluso podemos llegar a la misma solución empleando diversos métodos.

Veamos algún ejercicio sencillo:

Derive

Los ejercicios con rectas y puntos podemos resolverlos mediante el programa Derive.
En el CD-Rom del libro viene explicado cómo utilizar este programa para resolver estos ejercicios.

Dos aclaraciones:
a) La expresión para calcular la ecuación de una recta dado un punto (PX, PY) y el vector director (VX, VY) está mal escrita, os dejo como ejercicio calcular la expresión correcta (a partir de la ecuación continua de la recta quitar denominadores y agrupar términos)
b) En la versión 6 de Derive hay que especificar cuándo las variables son vectores
(Ir a Introducir > Dominio de una variable... > Vector)

Examen Vectores

1) Dados los vectores u, v, dibuja el vector 1/2·u + v. Expresa el vector a como combinación lineal de u, v.

Solución

2) Dados los vectores a(-3/4, 2), b(-2, 2), c(4, -1):
a) Obtén las componentes de a - 1/2·b y de -2c + b.
b) Expresa el vector c como combinación lineal de a y b.
Solución

3) Dados los vectores u(2, 3) y v(–3, 1), calcula:
a) (u + v)·u
b) u·(v·v)
Solución

4) Siendo u(5, –b) y v(a, 2), halla a y b sabiendo que u y v son ortogonales y que
Solución

5) Halla las coordenadas de un vector u sabiendo que forma un ángulo de 120º con a(–2, 4) y que los módulos de ambos son iguales.
Solución

 

Examen recuperación Números complejos

1) Halla en forma binómica y representa la solución obtenida:
    a) (–i + 1) (3 – 2i) (1 + 3i)
    b)
Solución

2) Calcula el valor de a y b para que se verifique:
Solución

3) Una de las raíces octavas de un número complejo, z, es – 1 + i. Halla el valor de z.
Solución

4) Calcula . Expresa el resultado en forma binómica.
Solución


5) El producto de dos números complejos es 2i y el cubo de uno de ellos dividido por el otro es 1/2. Hállalos.
Solución


6) Resuelve estas ecuaciones y expresa las soluciones en forma binómica:
    a) z⁴ + 8z = 0 Solución
    b) z² – 4iz – 5 = 0 Solución

Tema 8

Vamos a estudiar en este tema las relaciones entre puntos, rectas y entre puntos y rectas.
Para tener una visión global del tema podemos consultar el mapa conceptual:

Ángulo entre vectores

La fórmula del producto escalar:

u·v = u v cos(u, v)

nos permite calcular el ángulo entre vectores

Vectores perpendiculares

Dado un vector u(m, n) podemos ver que el vector v(-n, m) es perpendicular a u, su producto escalar vale 0

u·v = m(-n) + n·m = 0

Este resultado es muy útil para determinar vectores perpendiculares a uno dado.

Pruebas evaluativas vectores

He preparado una serie de pruebas sobre vectores:
Prueba A
Prueba B
Prueba C

Suerte.

Ejercicios tema 7

En las soluciones dadas hay dos ejercicios que precisan corrección. Son estos



Por otra parte aquí están todos los ejercicios resueltos (pdf, 218kb)

Producto escalar

Vamos con algunos ejercicios de producto escalar de vectores

Examen Números complejos

1) Halla en forma binómica y representa la solución obtenida:
  a) 3 + 2i (–1 + i ) – (5 – 4i )
  b)
Solución

2) Dados los complejos 2 – ai y 3 – bi, halla a y b para que su producto sea igual a 8 + 4i.
Solución

3) Calcula la cuarta potencia del número complejo
Solución

4) Calcula e interpreta gráficamente las soluciones
Solución

5) Si el producto de dos números complejos es –8 y dividiendo el cubo de uno de ellos entre el otro obtenemos de resultado 2, ¿cuánto valen el módulo y el argumento de cada uno?
Solución

6) Resuelve estas ecuaciones y expresa las soluciones en forma binómica:
  a) z³ + 8i = 0
  b) iz⁴ + 4 = 0
Solución

Pruebas evaluativas Tema 6

He ampliado los ejercicios de autoevaluación, ahora tenemos 3 opciones:
Prueba A
Prueba B
Prueba C
Espero que no sean muy difíciles.
Suerte.

Bases y coordenadas

Para trabajar con vectores es mucho más cómodo elegir una base y trabajar con las coordenadas de los vectores:

Tema 7 Vectores

Empezamos tema, los vectores.
Los vectores se utilizan habitualmente en física, ahora vamos a conocer más a fondo sus características y propiedades.
Empezamos con unos ejercicios fáciles: