Examen septiembre

jb
El examen de septiembre será el

Viernes 2 de septiembre a las 8:00 horas

Suerte a todos

Podéis consultar el calendario de exámenes de septiembre del
IES Santa Maria d'Eivissa
jb

Examen final, soluciones

jb

Matemáticas I

1.	a) Racionaliza y efectúa las operaciones: b) Halla el valor de x (positivo) en la expresión: log x2 = –4 Solución
2)	Resuelve: Solución
3)	Calcula los lados y los ángulos de un triángulo si sabemos: b = 12 m, c = 16 m, C = 50º. Solución
4)	Halla las coordenadas del vértice D de un paralelogramo ABCD, sabiendo que A(2, 3), B(6, 0) y C(8, 2). Solución
5)	Un supermercado utiliza una furgoneta para llevar a domicilio las compras de sus clientes. El precio de la furgoneta fue de 25.000 €. Se estima, además, que el coste de uso y mantenimiento es de 0,2 € por km. Determina: a) La función que da el precio total dependiendo de los km   recorridos. b) ¿A cuánto ha salido el km si la furgoneta es inservible cuando   ha recorrido 350.000 km? Solución
6)	a) Halla la ecuación de la recta tangente a la curva f(x) = 2x – 3x2   en el punto de abcisa x0 = 2. b) Halla los tramos en los que f(x) es creciente y decreciente. Solución
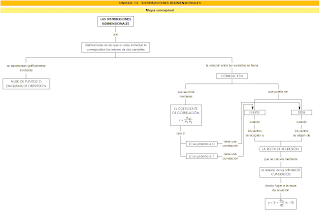
7)	Las notas obtenidas por un grupo de 5 alumnos y alumnas de 1.º de Bachillerato en un examen de matemáticas y en otro de inglés fueron las siguientes: Matemáticas 10 6 6 3 8 Inglés 9 7 5 4 9 Representa los datos en una nube de puntos y halla el coeficiente de correlación. ¿Cómo es la relación entre las dos variables? Solución

Nota: Haz un examen limpio, sin borrones. No utilizar lápiz (salvo gráficos).
jb

Examen final

jb
Os recuerdo que el examen final será el

Lunes 23 de mayo a las 17:30 horas

Suerte a todos
jb

Examen 3a evaluación, soluciones

jb

3ª evaluación

1)	Un comerciante vende un producto a 5 € la unidad. Si le encargan más de 10 unidades decide rebajar el precio: por cada x unidades cobra: Si suponemos que la función se amplía para cualquier valor real positivo: a) Halla a para que el precio varíe de forma continua. b) ¿A cuánto tiende el precio por unidad si se compran muchas   unidades? Solución
2)	Halla la derivada: a) f(x) = cos 3x b) $$f(x)=(x + 1)/(x − 1)$$ Solución
3)	Averigua cuáles son las asíntotas de la siguiente función y representa gráficamente la posición de la curva respecto a ellas: Solución
4)	Hemos preguntado a seis personas su peso y el número de calzado que usan, obteniendo los resultados que se recogen en la tabla: X: Peso 52 50 53 54 54 55 Y: Nº Calzado 35 36 37 38 39 36 Calcula la covarianza y el coeficiente de correlación. Solución
5)	En una urna, I, hay 5 bolas rojas y 7 bolas negras. En otra urna, II, hay 6 bolas rojas y 8 negras. Con probabilidad 1/3 elegimos la urna I; y, con probabilidad 2/3, elegimos la urna II, Extraemos una bola de la urna elegida. a) ¿Cuál es la probabilidad de que sea roja? b) Sabiendo que ha salido roja, ¿cuál es la probabilidad de que   fuera de la urna II? Solución

jb

Examen 3a Evaluación

jb
Os recuerdo que el examen de la tercera evaluación será el

Jueves 19 de mayo a las 16:00 horas

Suerte a todos
jb

Examen temas 13 y 14, soluciones

jb

Estadística y probabilidad

Se han medido dos características en una población mediante pruebas evaluables de 0 a 10 puntos, obteniendo los siguientes resultados en los primeros diez individuos:

X:	1	2	3	4	4	5	6	7	8	9
Y:	5	8	7	6	9	4	5	2	3	1

1)	Representa la nube de puntos correspondiente a esta distribución. Indica razonadamente cuál de los siguientes valores de r se ajusta mejor a esta distribución: r = 0,99;  r = 0,76;  r = –0,99;  r = –0,76 Solución
2)	Halla la recta de regresión de Y sobre X, indicando todos los pasos. Solución
3)	Sean A y B dos sucesos tales que: P[A' ∪ B'] = 0,7; P[A'] = 0,2; P[B] = 0,4. Halla P[A ∪ B] y P[A' ∩ B]. Solución
4)	En una academia hay 60 alumnos matriculados. La tercera parte de ellos van a clase de inglés y las otras dos terceras partes van a clase de informática. De los que van a inglés, un 40% también va a francés. De lo que van a informática, un 25% también va a francés. Si elegimos un alumno al azar: a) ¿Cuál es la probabilidad de que vaya a francés? b) Sabiendo que va a francés, ¿cuál es la probabilidad de que vaya   también a informática? Solución

Nota: Los ejercicios 1, 3 y 4 valen 2 puntos, el ejercicio 2 vale 4 puntos.
jb

Tema 14: Probabilidad

jb
Un vistazo global a la unidad, mapa conceptual:



Para consultar ejercicios sobre probabilidad, podéis revisar:

¤ Tema 14 Probabilidades
¤ Probabilidad
¤ Probabilidad (II)
¤ Probabilidad (III)
¤ Tema 14 Soluciones

Tenemos las soluciones a los ejercicios del libro: 1a parte, 2a parte.

En Matemáticas 1º Bachillerato tenéis muchos más recursos sobre este tema.

jb

Estadística y calculadora

jb
En este tema podemos hacer un buen uso de la calculadora:
las calculadoras científicas permiten calcular automáticamente casi todos los parámetros estadísticos, hay que saber utilizarlas.

Si tenéis una calculadora Casio y habéis perdido el manual, no tenéis excusa:

"Conoce bien a tu calculadora, ella puede ayudarte más de lo que imaginas"
jb

Tema 13: Distribuciones bidimensionales

jb
En la última parte del curso vamos a estudiar unos conceptos sencillos de estadística y probabilidad.

Primero el mapa conceptual de la unidad:



Unos enlaces para repasar la estadística:
Introducción a la estadística - Monografias.com
Elementos de probabilidad y estadística
Estadística 2º de Bachillerato - WikiDdS

Para consultar ejercicios sobre estadística, podéis revisar:

¤ Tema 13 Distribuciones bidimensionales
¤ Estadística
¤ Estadística (II)
¤ Estadística (III)
¤ Estadística (IV)
¤ Tema 13 Soluciones

Todas las soluciones de los ejercicios del libro.

En Matemáticas 1º Bachillerato tenéis muchos más recursos sobre este tema.

jb

Examen temas 11 y 12, soluciones

jb

Límites y derivadas

1)	Calcula los límites: a) b) Solución
2)	Un cultivo de bacterias comienza con 100 células. Sigue un crecimiento de acuerdo con la expresión y = 100 + 0,1t2 (t en minutos) durante 20 minutos. En ese momento se inyecta un inhibidor del crecimiento y a partir de este instante el crecimiento sigue la ley a) Halla el número de bacterias a los 20 minutos. b) Halla k para que sea una función continua. c) Si el experimento continúa indefinidamente, ¿qué sucederá con   el número de bacterias? Solución
3)	Halla la derivada: a)     b) Solución
4)	Un almacenista tiene 1.000 kg de manzanas que hoy puede vender a 60 céntimos de euro/kg. Cada día que pasa se estropearán 50 kg y el precio aumentará 10 céntimos de euro/kg. a) Escribe la ecuación que nos da el beneficio obtenido en la   venta, y, en función de los días que pasan hasta que vende las   manzanas, x. b) Representa la función obtenida, considerando que x puede   tomar cualquier valor x ≥ 0. c) Halla qué día debe vender para obtener un beneficio máximo. Solución
5)	Dada la función : a) Halla dónde es creciente y decreciente. b) Halla sus asíntotas y representa gráficamente la posición de la   curva respecto a ellas. Solución

jb

Tema 12: Derivadas

jb
Un vistazo global a la unidad, mapa conceptual:



Para consultar ejercicios sobre derivadas, podéis revisar:

¤ Tema 12 Derivadas
¤ Derivadas (II)
¤ Derivadas (III)
¤ Derivadas (IV)
¤ Derivadas (V)
¤ Derivadas (VI)
¤ Representación de funciones
¤ Representación de funciones (II)
¤ Tema 12 Soluciones

En YouTube encontraréis muchos videos de resolución de derivadas, por ejemplo:



Tenemos todas las soluciones de los ejercicios del libro.

En Matemáticas 1º Bachillerato tenéis muchos más recursos sobre este tema.

jb

Curso Derive

jb
Para estudiar estos temas podemos ayudarnos del programa Derive.

Puedes descargarte la versión 6.

Para conocer el programa puedes visitar este curso.
jb

Tema 11: Límites de funciones

jb
Un vistazo global a la unidad, mapa conceptual:



Para consultar ejercicios sobre límites, podéis revisar:

¤ Tema 11 Límites
¤ Tema 11 Límites de funciones. Continuidad y ramas ...
¤ Tema 11 Continuidad
¤ Límites
¤ Asíntotas
¤ Tema 11 Soluciones (y corrección de errores)

Y todas las soluciones de los ejercicios del libro.

En Matemáticas 1º Bachillerato tenéis muchos más recursos sobre este tema.

jb

Ex 2a Evaluación Soluciones

jb

Segunda Evaluación

1)	Dados los vectores u = (–1, 4), v = (m, n) y w = (2, –2) a) Calcula m y n para que u = 3v – 2w. b) Halla el ángulo que forman u y w. Solución
2)	Halla el valor de k para que las rectas r: 2x – 3y + 4 = 0 y s: –3x + ky – 1 = 0 sean perpendiculares. ¿Cuál es la pendiente de cada recta? Solución
3)	Halla las ecuaciones paramétricas y continua de la recta que pasa por A(5, –2) y es paralela a Solución
4)	Escribe la ecuación de la circunferencia con centro en el punto (2, –3) y que es tangente a la recta 3x – 4y + 5 = 0. Solución
5)	¿Cuánto vale la suma de los 100 primeros múltiplos de 7? Solución
6)	Halla algunos términos muy avanzados de la sucesión 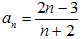e indica cuál es su límite Solución
7)	Las tarifas de una empresa de transportes son: • Si la carga pesa menos de 10 toneladas, una cantidad fija de   100 € más 40 euros por tonelada. • Si la carga pesa entre 10 y 30 toneladas, una cantidad fija de   200 € más 30 euros por tonelada (la carga máxima que   admiten es de 30 toneladas) a) Halla la expresión analítica de la función que expresa el precio   según la carga. b) ¿Cuál es su dominio? c) Representa la función. Solución

jb

Examen parcial 2a evaluación

jb

Temas 2 y 10

1)	En una progresión geométrica de razón positiva, conocemos a3 = 8 y a5 = 0’5. a) Calcula a1 y la razón. b) Halla la suma de sus infinitos términos. Solución
2)	En un cine, la segunda fila de butacas está a 10 m de la pantalla y la séptima fila está a 16 m. ¿En qué fila debe sentarse una persona que le guste ver la pantalla a una distancia de 28 m? Solución
3)	Representa la función Solución
4)	Dadas las funciones , calcula: a) b) Solución
5)	Las tarifas de una empresa de transportes son: 40 euros por tonelada de carga si esta es menor o igual a 10 t. Si la carga es mayor que 10 t, se restará, de los 40 euros, tantos euros como toneladas sobrepasen las 10. a) Dibuja la función ingresos de la empresa según la carga que   transporte (carga máxima: 30 t). b) Obtén la expresión analítica. Solución

jb

Tema 10: Funciones elementales

jb
Un vistazo global a la unidad: mapa conceptual



Para consultar ejercicios sobre funciones, podéis revisar:

¤ Tema 10 Funciones elementales
¤ Funciones (II)
¤ Funciones (III)
¤ Tema 10 (I)
¤ Tema 10 (II)
¤ Tema 10 (III)

Y todas las soluciones de los ejercicios del libro.

En Matemáticas 1º Bachillerato tenéis muchos más recursos sobre este tema.

jb

Examen Geometría (Soluciones)

jb

Geometría

1)	Dados los vectores a = y b = (1, x) a) Si x = 1, halla el ángulo entre ambos vectores. b) ¿Para qué valores de x son perpendiculares? Solución
2)	Obtén las ecuaciones paramétricas de la recta r, que pasa por P(3, –2) y es perpendicular a la recta 2x – y + 4 = 0. Estudia la posición relativa de la recta r, obtenida anteriormente, con la recta:   Solución
3)	Halla el ángulo que forman las rectas:     y   s: x + y – 1 = 0 Solución
4)	Obtén el lugar geométrico de los puntos  P  del plano que equidistan de las rectas:   r : 3x – 2y – 1 = 0   y   s : 2x + 3y + 2 = 0 ¿Qué obtienes? Solución
5)	Escribe la ecuación de la circunferencia con centro en el punto (2, –3) y que es tangente a la recta 3x – 4y + 5 = 0. Solución

jb

Tema 2: Sucesiones

jb
Un vistazo global a la unidad: mapa conceptual



Para consultar ejercicios sobre sucesiones, podéis revisar :

¤ Tema 2 Sucesiones
¤ Sucesiones (I)
¤ Sucesiones (II)
¤ Sucesiones (III)
¤ Sucesiones (IV)

Y todas las soluciones de los ejercicios del libro.

En Matemáticas 1º Bachillerato tenéis más recursos sobre este tema.



Sobre la sucesión de Fibonacci tenemos algunas páginas interesantes:

¤ Wikipedia
¤ La sucesión de Fibonacci y la naturaleza
¤ Fibonacci en la naturaleza
¤ Ciencia y conocimiento

jb

Examen temas 7, 8 y 9

jb
A petición de los alumnos y para facilitar la superación de la materia de este curso, habrá un examen parcial de geometría.
El examen de los temas 7, 8 y 9 será el
martes, día 25 a las 17:50
jb

Tema 9: Cónicas

jb
Para empezar el tema: planteamiento

Programación

Ejercicios con Derive

Criterios de evaluación

Un vistazo global a la unidad: mapa conceptual



Para consultar ejercicios sobre geometría, podéis revisar:

¤	Tema 9 (I)
¤	Tema 9 (II)
¤	Tema 9 (III)
¤	Tema 9 (IV)
¤	Tema 9 (V)
¤	Examen Tema 9

Tenemos disponibles las soluciones del tema 9

En Matemáticas 1º Bachillerato tenéis más recursos sobre este tema.

jb